电力系统pv曲线算法实例图解
来源:电工天下时间:2017-03-09 19:53:07 作者:老电工手机版>>
【电力系统pv曲线算法实例图解】
系统的潮流方程可用式(1)表示。式中λ为负荷增长率,b为负荷增长方式。
f(x)-λ.b=0 (1)
连续潮流法是假设系统处于准静态的状态下,随负荷的缓慢增加,不断求解潮流方程,从而描绘出系统的PV曲线。常规潮流总是沿着PV曲线从上一个解向下一个解迭代收敛。在极限点附近,系统方程各变量的一阶偏导趋近于零,雅可比矩阵变得奇异。
因此,只要合理地改变潮流方程的收敛方向,雅可比矩阵就可以不再奇异。为防止潮流迭代一次之后回到原常规方法的收敛方向上,不但要合理地进行预估而且必须增加一维潮流方程,使潮流从N+1维空间向精确解收敛。该方法在数学上称为延拓法。文献〔4〕以式(2)为增广的潮流方程:
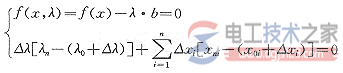
(2)
式中增加的一维方程是潮流解与预估值的正交方程,如图1所示。
Δλ和Δxi是每次潮流迭代前的预估值,在迭代时是常量〔4〕。该方法率先提出了利用改变收敛方向的方法解决极限点附近潮流不收敛的问题,但在实现上会有一些问题。
首先,从图1中可以发现接近极限点后,预估值的正交平面可能与PV曲线无法相交(图中下标s和b分别表示小步长和大步长),此时式(2)无解,在步长稍大时该现象比较明显。
其次,由于增广的雅可比矩阵增加的一维完全是常数矢量,所以新方程组只是在N+1维空间中以不同的系统流形切面(N维超平面)向极限点逼近,并没能充分利用增加的一维空间。
从这方面讲,该方法在极限点附近有可能迭代不收敛。
此外,由于文献〔4〕的变步长方法依赖于常规雅可比矩阵形成的方程组。在其接近奇异时解方程的误差会造成预估点不准确,对其收敛性也有影响。

图1 延拓法示意图
Fig.1 Illustration of the continuation method
考虑以上几点,以弧长公式重新形成第N+1维方程,并构造增广潮流方程:
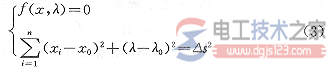
也可以根据各节点的重要性不同分配权重,形成伪弧长公式并将其作为第N+1维方程:
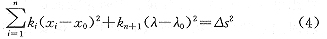
式中x0和λ0分别为PV曲线中上一个潮流解的电压值和负荷增长率;ki为对各参量分配的权重。
新方程组对应的雅可比矩阵分别如下:
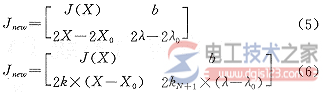
式中 J(X)为原来的雅可比矩阵。
有严格的数学理论证明〔5〕,新的雅可比矩阵充分利用了增广的第N+1维空间,在功率极限点(简单奇点)处不再奇异。利用新的潮流方程组可以求出整支PV曲线,而不会遇到潮流发散的问题。
由于采用了弧长或伪弧长公式作为负荷增长率λ的控制方程,使该方法对于λ的变化采取了自动变步长的方法。
在负荷较低时,电压变化率ΔX较小,相应的负荷增长率Δλ就比较大;而当接近于功率极限点时电压变化率突然增大,对应的负荷增长率变小,曲线上的点就比较密。
方程中弧长Δs的确定对程序有一定影响:若Δs取得较大,则PV曲线在极限点附近不够光滑,极限点也有一定误差(但相对其他方法误差仍然不大),弧长太大有可能导致方程无解;若取得太小,虽然曲线光滑,极限点也很精确,但运算量很大。程序中在每步潮流运算之后求取常规雅可比矩阵的奇异值,以确定当前点离极限点的距离。
以较大的弧长开始迅速通过低负荷PV曲线较平坦的部分,当常规雅可比矩阵的最小奇异值小于一定值之后,减小弧长的值使求得的曲线细密精确。
由于奇异值分析对系统电压稳定的分析控制也有重要意义〔6〕,所以相对而言弧长控制在程序中非常容易。
为加快程序运行速度,引入了预估校正技术〔7〕。先通过插值法对下一个潮流值进行预估,再由潮流方程进行求解校正,使得运算速度大大加快,一般2到4次迭代就可以得到精确结果(ε=10-5)。
相关文章电力系统的负荷特性图解

有关电力系统的负荷特性,电力系统的总负荷为电力系统中各个用电设备消耗功率的总和,电力系统的负荷曲线,用于确定系统用电设备全年的用电量。
时间:2022-09-13 13:22:42
电力负荷调度的经验总结

有关电力负荷调度的经验总结,负荷调度模式研究聚焦电价机制、合约机制、需求侧竞价以及有序用电等内容,柔性负荷调度模式和控制策略研究的问题等。
时间:2022-09-12 12:49:01
负荷曲线是什么,计算负荷的方法图解
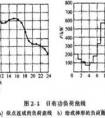
有关负荷曲线与计算负荷的方法,负荷曲线是电力负荷随时间变化的曲线,分为日负荷曲线、月负荷曲线、年负荷曲线等,根据负荷系统系数计算负荷的方法。
时间:2022-09-10 07:00:26
一文看懂短路电流的简化计算法
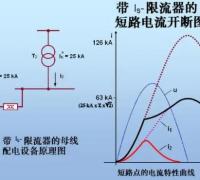
正确计算短路电流十分困难,一些设计手册提供了简化计算的图表,用起来比较方便。但手边一时没有设计手册怎么办,以下介绍一种 “口诀式”的计算方法,只要记牢7句口诀,即可掌握短路电流计算方法。
时间:2022-03-19 09:09:41
电力单位符号大全

电能的国际单位是焦耳,符号是J,常用单位为千瓦时,符号为KW·h,在生活中俗称为“度”。【电力计量单位:度】度是电量的常用单位,即千瓦时,符号为kW·h,功率为1000瓦的设备一小时的耗电量为1度电。
时间:2022-03-16 08:47:16
电力负荷的分级分类及高层建筑用电负荷

电力负荷的分级分类及高层建筑用电负荷的知识,按对供电可靠性要求的负荷分类,有一级负荷、二级负荷与三级负荷,按工作制的负荷分类,高层建筑用电负荷分类等。
时间:2020-04-29 14:37:05
企业供配电系统电力负荷如何计算?
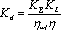
企业供配电系统电力负荷的计算方法,将供配电系统中各电气设备所在点的电力负荷进行计算,包括负荷系统数,线路供电效率,用电设备组在实际运行功率时的平均效率等。
时间:2020-04-29 14:31:02
如何计算负荷?电力负荷的实用计算方法
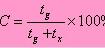
电力负荷的计算方法,包括短时运行工作制,断续周期工作制等,电力负荷的实用计算方法,分为需要系数法,三相计算负荷的确定法等。
时间:2020-04-29 14:30:58
- 上一篇:线电压与相电压的定义与区别
- 下一篇:电动势与路端电压的区别详解